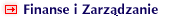|
Analiza fundamentalna podstawą budowy portfela papierów wartościowych | Prof.dr hab. Waldemar Tarczyński | 2002.09.29 |
W klasycznej analizie portfelowej teoria Markowitza była podstawą większości koncepcji budowy optymalnego portfela papierów wartościowych. Praktycznie wszystkie propozycje uwzględniają dwie podstawowe charakterystyki wykorzystywane przez inwestorów na rynku kapitałowym – stopę zwrotu z inwestycji i ryzyko inwestycji. Analizując rozwój historyczny technik konstruowania portfela papierów wartościowych, można stwierdzić, że nie pojawiają się nowe propozycje przyjmujące te wskaźniki. Częściej rozpatruje się zasadność klasycznego podejścia konstruowania klasycznych portfeli, weryfikację hipotezy efektywności rynku czy teorię chaosu, która burzy paradygmat rozkładów normalnych lub quasi-normalnych na rynkach kapitałowych. W tym artykule przedstawiono koncepcję konstruowania fundamentalnego portfela papierów wartościowych, która może być pewną alternatywą dla podejścia klasycznego.
1. Fundamentalne kryterium budowy portfela papierów wartościowych
Oceniając klasyczne koncepcje budowy portfela papierów wartościowych z punktu widzenia pragmatyki, można stwierdzić, że są to techniki analiz i dokonywania inwestycji długoterminowych. Wynika to przede wszystkim z małej elastyczności portfela papierów wartościowych. Bezcelowe jest konstruowanie portfela, gdy jego budowa może zająć czasami nawet kilka tygodni, a zmiana nastąpi na przykład po miesiącu. Nawet jeżeli stwierdzimy, na podstawie oceny aktualnej sytuacji rynkowej, konieczność przekonstruowania portfela, to praktyczne przeprowadzenie tego procesu, z uwagi na ograniczoną płynność giełdy papierów wartościowych (na Giełdzie Papierów Wartościowych w Warszawie przeciętnie na jednym notowaniu w obrocie jest 1% akcji każdej spółki), jest niemożliwe w krótkim okresie. Wydaje się zatem oczywiste, że portfel papierów wartościowych powinien być konstruowany długoterminowo. Z analizy giełdy wynika, że kryterium stopy zwrotu i ryzyka wyznaczanego na podstawie koncepcji wariancji stopy zwrotu nie są najlepszymi miarami ze względu na ich niestabilność. Jest to szczególnie widoczne na rynkach rozwijających się (do takich należy też rynek polski), z niewielką płynnością, gdzie klasyczne portfele nie pozwalają na osiąganie ponadprzeciętnych przychodów. Jest to przyczyna poszukiwania nowych rozwiązań, pozwalających na budowanie portfela papierów wartościowych w sposób naturalny, wykorzystującego długoterminowe podstawy do decyzji inwestycyjnej. Wydaje się, że celowe może być połączenie metod analizy fundamentalnej z ideą konstruowania portfela papierów wartościowych. Nie jest to bezpośrednio możliwe, ponieważ analiza fundamentalna jest zbyt obszerna i sformalizowanie jej na potrzeby budowy portfela wymaga znacznych uproszczeń. Analiza fundamentalna jako typowa technika analiz na potrzeby inwestycji długoterminowych wydaje się być dobrą podstawą do konstruowania portfela papierów wartościowych. Problemem, który musi zostać rozwiązany jest doprowadzenie wieloelementowych rezultatów analizy fundamentalnej do postaci umożliwiającej wykorzystanie jej do budowy portfela. Gwarancją rozwiązania tak postawionego problemu jest zaproponowana taksonomiczna miara atrakcyjności inwestycji TMAI.
2. Model fundamentalnego portfela papierów wartościowych
Nowa koncepcja konstruowania portfela papierów wartościowych jest propozycją budowania fundamentalnego długoterminowego portfela papierów wartościowych, uwzględniającego ważne zalety analizy fundamentalnej, czyli uwzględniającego rzeczywistą siłę spółek kosztem rezygnacji z podmiotów słabych z finansowo-ekonomicznego punktu widzenia, określanych mianem spółek spekulacyjnych. Portfel zbudowany na takich podstawach będzie stabilny i bezpieczny. Dla inwestorów długoterminowych zalety takiego podejścia są oczywiste. Zasadniczym kryterium podlegającym optymalizacji jest suma wartości syntetycznych miar opisujących siłę fundamentalną spółek wchodzących w skład portfela ważona udziałami akcji w portfelu. Wartość tak pojmowanego kryterium jest maksymalizowana. Taka konstrukcja funkcji celu ma zapewnić stabilność i bezpieczeństwo portfela w długim okresie. Pierwsze propozycje konstruowania takiego portfela można znaleźć w moich pracach [1995a, 1995b, 1996, 1997]. Etapy konstruowania fundamentalnego portfela papierów wartościowych przedstawiono na rysunku 1. Zaproponowane podejście umożliwia obiektywną ocenę kondycji finansowo-ekonomicznej spółek giełdowych i skonstruowanie portfela papierów wartościowych uwzględniającego ich siłę fundamentalną i długoterminowy charakter inwestycji. Na tak zbudowanym portfelu papierów wartościowych można dalej eksperymentować, na przykład zmierzając do opracowania uniwersalnych i stabilnych kryteriów dla syntetycznej miary i warunków ograniczających, które będą niewrażliwe na etap rozwoju rynku kapitałowego w danym kraju.
Rys. 1. Etapy konstruowania fundamentalnego portfela papierów wartościowych
Źródło: opracowanie własne.
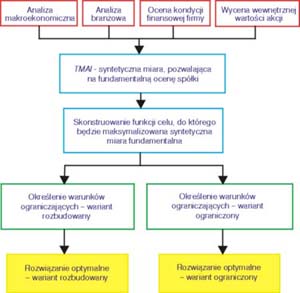
W proponowanej metodzie budowy fundamentalnego portfela papierów wartościowych wartości TMAI są kryterium podlegającym optymalizacji. Jest to zasadnicza zmiana w stosunku do klasycznych koncepcji opartych na stopie zwrotu i ryzyku. Portfel wykorzystujący kryterium TMAI jest optymalny z fundamentalnego punktu widzenia, czyli wybiera układ najlepszy ze względu na kondycję ekonomiczno-finansową spółek. Proponowana funkcja celu i warunki ograniczające w wariancie rozbudowanym może zostać zapisana następująco:
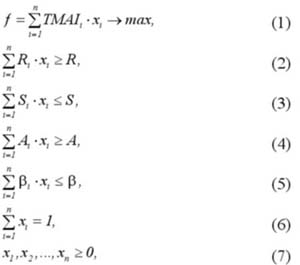
TMAIi – taksonomiczna miara atrakcyjności inwestycji w i-tą spółkę, xi – udział akcji i-tej spółki w portfelu, Ri – tygodniowa stopa zwrotu dla i-tej spółki, R – pożądana przez inwestora średnia tygodniowa stopa zwrotu portfela, Si – tygodniowe ryzyko inwestycji dla i-tej spółki wyznaczone jako odchylenie standardowe stopy zwrotu, S – akceptowane przez inwestora średnie tygodniowe ryzyko portfela, Ai – tygodniowy współczynnik skośności akcji dla i-tej spółki wyznaczony według wzoru:
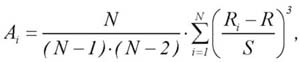
A – średni tygodniowy współczynnik skośności dla wszystkich spółek branych pod uwagę przy konstruowaniu portfela, bi – miesięczny współczynnik beta dla i-tej spółki wyznaczony jako ocena parametru strukturalnego równania liniowego stopy zwrotu i-tej akcji względem stopy zwrotu indeksu giełdy, b – średni miesięczny współczynnik beta dla wszystkich spółek branych pod uwagę przy konstruowaniu portfela, n – liczba spółek, N – liczba okresów na podstawie, których wyznacza się stopę zwrotu, ryzyko i asymetrię.
W wariancie rozbudowanym zaproponowany model wymaga nałożenia kilku dodatkowych ograniczeń oraz wyjaśnienia wystąpienia niektórych warunków ograniczających. Pierwsze, to ograniczenie potencjalnych papierów wartościowych mogących wejść w skład portfela do tych, dla których w przyjętym okresie analizy stopa zwrotu jest większa od zera. Oczywiście, w skrajnym przypadku można pominąć to ograniczenie i do analiz przyjąć wszystkie papiery wartościowe dostępne na rynku. Można wykorzystać też formalne kryteria, jak na przykład analizę dyskryminacyjną, która pozwala na wyodrębnienie grupy spółek spełniających określone warunki2 . Drugie, to zdefiniowanie okresu objętego analizą. Przyjęta w modelu zasada tygodniowych odcinków czasu nie musi być kanonem. Okres ten może być dłuższy lub krótszy, co jest uzależnione przede wszystkim od charakteru inwestycji. Generalnie przy długookresowym charakterze portfela wynikającym z jego istoty merytorycznej najkrótszy okres powinien być tygodniowy, zaś najdłuższy miesięczny. Trzecie, to konieczność określenia już na początku poziomu akceptacji ryzyka przez inwestora oraz oczekiwane przez niego stopy zwrotu z inwestycji. Model jest w tym zakresie bardzo elastyczny. Wartości R i S pożądane przez inwestora mogą być przyjęte zgodnie z efektem portfelowym stopy zwrotu i efektem portfelowym ryzyka, czyli R j ako minimalna stopa zwrotu ze spółek branych pod uwagę przy budowie portfela, S jako maksymalne odchylenie standardowe stopy zwrotu ze spółek branych pod uwagę przy budowie portfela. Jako wielkości graniczne można też przyjąć poziomy tych miar wyznaczone w inny sposób (np. średnia arytmetyczna ze stóp zwrotu i ryzyk dla spółek branych pod uwagę przy konstruowaniu portfela lub stopa zwrotu i ryzyko rynku mierzone indeksem giełdowym). Jeżeli chodzi o warunki ograniczające (2), (3), (6) ─ udziały poszczególnych akcji w portfelu sumują się do jedności, i (7), są one oczywiste i nie wymagają wyjaśnień. Warunek (4) jest konsekwencją faktu, że stopa zwrotu dla danej spółki w analizowanym okresie może mieć rozkład asymetryczny i wówczas ograniczenie się tylko do stopy zysku i ryzyka może nie być wystarczające. Generalnie inwestor powinien wybierać akcje, dla których rozkład jest prawostronnie asymetryczny. W takiej sytuacji spadki możliwych stóp zwrotu poniżej wartości oczekiwanej nie są duże, ale za to istnieje możliwość osiągnięcia stóp zwrotu znacznie wyższych od wartości oczekiwanej stopy zwrotu. Jest to pewne rozszerzenie zasady maksimum zysku i minimum ryzyka. W praktyce inwestor powinien dążyć do maksymalnej prawostronnej asymetrii. Warunek (5) pozwala na uwzględnienie ryzyka specyficznego dla danego papieru wartościowego. Wyznaczony na podstawie linii charakterystycznej dla papieru wartościowego, pozwala na wskazanie, w jakim stopniu stopa zwrotu akcji reaguje na zmiany stopy zwrotu wskaźnika rynku, czyli na zmiany zachodzące na rynku. W uproszczeniu współczynnik beta może być traktowany jako miara ryzyka rynkowego danej akcji. Pomimo, że miara ta występuje jako zmienna diagnostyczna w rozszerzonej koncepcji TMAI ze względu na jej znaczenie i wykorzystywanie na rynku przez dość dużą liczbę inwestorów należy ją również umieścić w najbardziej rozbudowanej wersji warunków ograniczających. Stopę zwrotu i ryzyko portfela wyznaczonego wzorami (1)─ (7) można obliczyć według wzorów:
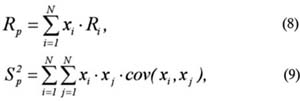
gdzie: Rp – stopa zwrotu portfela składającego się z N akcji, Sp2 – wariancja portfela, xi – udział ceny zakupu i-tej akcji spółki w cenie zakupu portfela, Ri – stopa zwrotu i-tej akcji, N – liczba akcji w portfelu, Si – odchylenie standardowe stopy zwrotu i-tej akcji, cov(xi,xj) – kowariancja między i-tą i j-tą akcją.
Skorzystanie ze wzorów (8) i (9) pozwala na porównanie fundamentalnego portfela papierów wartościowych z klasycznymi portfelami konstruowanymi zgodnie z zasadami teorii Markowitza. Wadą takiego sposobu pomiaru stopy zwrotu i ryzyka, zarówno w klasycznych modelach, jak i w podejściu fundamentalnym, jest fakt, że wielkości te nie są prognozą a jedynie egzemplifikacją przeszłości. Idealne byłoby rozwiązanie wykorzystujące prognozy. Wartości obliczone na podstawie danych historycznych, jak pokazuje praktyka, nie są najcelniejsze i należy do nich podchodzić z dużą rozwagą. Proponowany model nie uwzględnia możliwości krótkiej sprzedaży (warunek (7). Usunięcie tego warunku z modelu będzie równoznaczne z dopuszczeniem zastosowania w praktyce krótkiej sprzedaży (udziały akcji w portfelu mogą być ujemne, ale w dalszym ciągu ich suma będzie równa jedności). Z dotychczasowych moich badań i symulacji na Giełdzie Papierów Wartościowych w Warszawie wynika, że w praktyce polskiego rynku kapitałowego najlepiej sprawdza się model z funkcją celu (1) i warunkami ograniczającymi (2), (3), (6) i (7).
W zasadzie formuła modelu nie narzuca tu ostatecznych ograniczeń i w zależności od preferencji inwestora można wprowadzić do modelu również inne warunki ograniczające. Należy jednak pamiętać, ze najważniejsza informacja jest zawarta w warunkach (2) i (3) i dalsze rozbudowywanie modelu wcale nie musi prowadzić (i tak jest najczęściej) do poprawy jego jakości, która jeżeli już wystąpi to nie jest na tyle istotna, aby uzasadniało to komplikowanie modelu nowymi warunkami ograniczającymi. W przypadku samych wartości TMAI występujących w funkcji celu, aby uchwycić jak najlepiej kondycję firm można wyznaczyć wartości poszczególnych wskaźników ekonomiczno-finansowych jako pewną średnią z trzech lub pięciu ostatnich lat, co faktycznie odda istotę kondycji firmy. Jeśli mamy trudności z uzyskaniem wiarygodnych prognoz tych wielkości takie podejście jest bardzo wskazane. Można wreszcie podjąć się próby analizowania ciągu wartości TMAI dla firmy za kilka okresów i przyjmowanie do modelu również pewnych średnich tych wielkości. W przypadku stabilnej gospodarki i rynku kapitałowego w danym kraju można zaproponować prognozowanie wartości TMAI i na tej podstawie dopiero budowanie portfela fundamentalnego. Zgodnie ze schematem zamieszczonym na rysunku 1 zbudowano fundamentalny portfel papierów wartościowych. W pierwszym kroku zostały wyznaczone wartości TMAI syntetycznej miary, określającej siłę fundamentalną dla wybranych spółek notowanych na Giełdzie Papierów Wartościowych w Warszawie. Technikę wyznaczania wartości TMAI przedstawiono w pracach: Tarczyński [1994, 2001, 2002]. Wartości TMAI dla wybranych spółek zamieszczono w tabeli 1.
Tabela 1. Wartości stopy zwrotu, ryzyka mierzonego odchyleniem standardowym oraz TMAI dlawybranych spółek na dzień 31 grudnia 2001 roku
| Wyszczególnienie |
Ri |
Si |
TMAIi |
Rangi |
| COMPLAND |
0,0085 |
0,0986 |
0,522 |
2 |
| SWIECIE |
0,0084 |
0,0671 |
0,393 |
4 |
| PEKAO |
0,0044 |
0,0439 |
0,438 |
3 |
| PROKOM |
0,0022 |
0,0960 |
0,318 |
6 |
| BPHPBK |
0,0023 |
0,0480 |
0,226 |
7 |
| AGORA |
0,0007 |
0,0853 |
0,523 |
1 |
| INGBSK |
0,0020 |
0,0477 |
0,206 |
8 |
| BRE |
-0,0002 |
0,0529 |
0,374 |
5 |
| BUDIMEX |
-0,0005 |
0,0554 |
0,006 |
9 |
Źródło: obliczenia własne.
Dysponując wartościami TMAI, można przystąpić do budowy fundamentalnego portfela papierów wartościowych. Model przyjmie zatem postać:

Wykorzystując dane zawarte w tabeli 1 oraz powyższy model, oszacowano skład fundamentalnego portfela papierów wartościowych. Do obliczeń wykorzystano narzędzie solver z arkusza kalkulacyjnego Excel MS Office 2000. Rezultaty obliczeń są następujące:
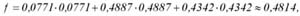
realizacja ograniczeń dla tego rozwiązania:

Z otrzymanych rezultatów wynika, że fundamentalny portfel papierów wartościowych dla badanego okresu powinien składać się z 49% akcji spółki PEKAO, 43% akcji spółki AGORA i 8% akcji spółki COMPLAND. Stopa zwrotu tego portfela i ryzyko zgodnie z wzorami (8) i (9) są odpowiednio równe:

Teoretycznie inwestor konstruując taki fundamentalny portfel chcąc ocenić jego podstawowe parametry (oczekiwaną stopę zwrotu i oczekiwane ryzyko) zgodnie z procedurą stosowaną w klasycznych modelach (Markowitza i Sharpe’a) powinien spodziewać się średniej tygodniowej stopy zwrotu na poziomie około 0,3% przy oczekiwanym średnim tygodniowym ryzyku równym 5,4%. Daje to spodziewany przedział realizacji inwestycji w ujęciu tygodniowym od –5,1% do 5,7%.
3. Ocena efektywności fundamentalnego portfela papierów wartościowych
W klasycznym portfelu papierów wartościowych zbudowanym za pomocą modelu Markowitza lub Sharpe’a ocena jego efektywności może być przeprowadzona na podstawie porównania oczekiwanej stopy zwrotu jaką miał portfel w momencie budowy z faktycznie zrealizowaną stopą zwrotu po upływie założonego okresu. Inny sposób może polegać na śledzeniu zmian w czasie stopy zwrotu portfela i odnoszenie tych zmian do normy jaką jest oczekiwana stopa zwrotu. Najczęściej do konstrukcji portfela w ujęciu klasycznym wykorzystuje się dane historyczne oraz zakłada się rozkład normalny stopy zwrotu i występowanie prawidłowości statystycznych w zakresie kształtowania się stóp zwrotu. Przy spełnieniu tych założeń, które w praktyce spełnione są rzadko, oczekiwana stopa zwrotu może być tożsama z rzeczywistością. Niestety w warunkach niestabilnego i rozwijającego się rynku kapitałowego takie podejście nie jest najlepsze. Wartość oczekiwana nie jest dobrą prognozą stopy zwrotu i rzadko realizuje się w przyszłości. Ideałem byłoby zastąpienie w takiej sytuacji stopy zwrotu i ryzyka papierów wartościowych, czyli informacji koniecznych do zbudowania portfela, ich prognozami. Niestety nie jest znana dostatecznie dobra metoda prognozowania, przy której błąd prognozy nie przekreślałby jej użyteczności. Znane metody w pewnych sytuacjach sprawdzają się świetnie, w innych zawodzą całkowicie. Inwestor niestety nie jest w stanie dokładnie przewidzieć, którą metodę kiedy stosować. Jeżeli dana sytuacja już się zdarzy, to jest po prostu za późno na decyzję inwestycyjną. Z tego względu najczęściej pozostaje się przy podejściu opisanym na początku tego podrozdziału. Zupełnie inaczej wygląda sytuacja fundamentalnego portfela papierów wartościowych. Dane wykorzystane do jego zbudowania tu „fundamenty”, które tworzyły się od kilku lat (jak wspomniano wcześniej jest to najczęściej okres od 3 do 5 lat). Mniej istotne są historyczna i aktualna stopa zwrotu oraz jej ryzyko mierzone odchyleniem standardowym. Ponieważ przyszłe korzyści nie mają wynikać z prawidłowości kształtowania się w przeszłości stóp zwrotu ale z siły fundamentalnej spółki, która uzewnętrzni się w długim horyzoncie czasowym. Przy takim podejściu również założenie o rozkładzie normalnym stóp zwrotu nie musi być spełnione. Jest to bardzo duża zaleta portfela fundamentalnego, która daje mu dużą przewagę merytoryczną w długim horyzoncie czasowym. Faktyczną efektywność portfela fundamentalnego można ocenić w tym przypadku odnosząc wartość portfela w momencie jego sprzedaży lub dowolnym momencie w przyszłości do kosztu jego zakupu. Jest to nic innego jak faktyczna stopa zwrotu portfela:
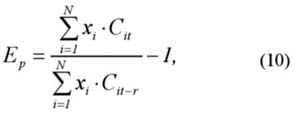
gdzie: Ep – efektywność portfela mierzona względną stopą zwrotu, xi – udział i-tej akcji w portfelu, Cit - r – cena i-tej akcji w okresie wcześniejszym od bieżącego o r okresów (koszt zakupu), Cit – cena i-tej akcji w momencie sprzedaży, N – liczba akcji w portfelu.
Tak otrzymana wielkość może być porównywana z wartością depozytów i wolnej od ryzyka stopy zwrotu na rynku w analogicznym okresie, stopą zwrotu indeksów giełdowych itp. Oczywiście wartość Ep wyższa od normy będzie oznaczała, że dany fundamentalny portfel jest efektywny w sensie przyjętej normy. W modelu Markowitza i jego pochodnych taką normą jest zazwyczaj poziom ryzyka akceptowalny przez inwestora lub (co się zdarza rzadziej) poziom oczekiwanej stopy zwrotu z portfela. Aby zaprezentować takie podejście w praktyce oceńmy efektywność portfeli zbudowanych według modelu Markowitza i Sharpe’a z efektywnością portfela fundamentalnego. Portfele zostały zbudowane na tej samej populacji spółek dla danych za ten sam okres zgodnie z zasadami właściwymi dla każdej z metod. Model Markowitza zbudowano według następujących wzorów:

gdzie: Sp2 – wariancja portfela (miara ryzyka portfela), xi, xj – udziału akcji w portfelu, cov(xi,xj) – kowariancja między i-tą i j-tą akcją. Rp – stopa zwrotu z portfela, R0 – zadany przez inwestora oczekiwany minimalny poziom stopy zwrotu, N – liczba akcji wykorzystanych do budowy portfela.
W przypadku modelu Sharpe’a jedyna różnica polega na innym wyrażeniu ryzyka przy niezmienonych pozostałych powyższych zapisach. W koncepcji tej wykorzystuje się jednoczynnikowy model regresji, w którym stopa zwrotu z akcji jest objaśniana stopą zwrotu z rynku. Współczynnik stojący przy zmiennej opisującej stopę zwrotu rynku jest nazywany współczynnikiem beta i służy do wyrażenia ryzyka. Formalnie zatem różnica między modelem Markowitza i Sharpe’a polega na innym zapisie funkcji celu co wyraża następująca relacja:
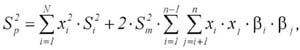
gdzie: Sm2 – wariancja rynku (wariancja stopy zwrotu dla indeksu giełdowego), β – miara ryzyka dla i-tej i j-tej akcji, pozostałe oznaczenia jak w powyższych wzorach. Oznacza to, że w klasycznej macierzy wariancji i kowariancji jaka jest wykorzystywana w modelu Markowitza kowariancje zastąpione są iloczynem
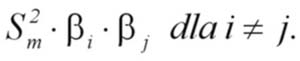
Badaniem objęto spółki tworzące w marcu 2002 roku indeks giełdowy WIG20. Warunkiem wstępnym zakwalifikowania danej spółki do analizy była dodatnia tygodniowa stopa zwrotu za okres od stycznia 2000 roku do grudnia 2001 roku. Warunek ten spełniło 9 spółek. Korzystając z podanych powyżej wzorów dla różnych poziomów średniej tygodniowej stopy zwrotu portfela R0 poczynając od 0,0010 do 0,0085 wyznaczono minimalną wartość Sp2 oraz odpowiadające jej udziału poszczególnych akcji w portfelu. Wyniki tych obliczeń dla modelu Markowitza i Sharpe’a zamieszczono w tabeli 2.
Tabela 2. Stopa zwrotu i ryzyko dla portfeli zbudowanych za pomocą modelu Markowitza i Sharpe’a
| Rp |
Sp |
COMPLAND |
SWIECIE |
PEKAO |
PROKOM |
BPHPBK |
AGORA |
INGBSK |
BRE |
BUDIMEX |
| 0,0010 |
0,0339 |
0,0000 |
0,0000 |
0,1062 |
0,0000 |
0,1357 |
0,0086 |
0,2000 |
0,2624 |
0,2872 |
| 0,0020 |
0,0314 |
0,0000 |
0,0575 |
0,1985 |
0,0000 |
0,1590 |
0,0000 |
0,2032 |
0,1800 |
0,2017 |
| 0,0030 |
0,0306 |
0,0000 |
0,1366 |
0,2495 |
0,0000 |
0,1694 |
0,0000 |
0,2121 |
0,1099 |
0,1225 |
| 0,0040 |
0,0314 |
0,0177 |
0,2065 |
0,2910 |
0,0000 |
0,1806 |
0,0000 |
0,2223 |
0,0338 |
0,0481 |
| 0,0050 |
0,0336 |
0,0607 |
0,2807 |
0,3164 |
0,0000 |
0,1482 |
0,0000 |
0,1941 |
0,0000 |
0,0000 |
| 0,0060 |
0,0383 |
0,1127 |
0,3785 |
0,3432 |
0,0000 |
0,0533 |
0,0000 |
0,1122 |
0,0000 |
0,0000 |
| 0,0070 |
0,0451 |
0,1675 |
0,4774 |
0,3551 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
| 0,0080 |
0,0544 |
0,2528 |
0,6380 |
0,1093 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
| 0,0085 |
0,0742 |
0,6889 |
0,3111 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
| Model Sharpe’a |
| 0,0010 |
0,0313 |
0,0000 |
0,0000 |
0,0820 |
0,0000 |
0,1527 |
0,0000 |
0,2316 |
0,2621 |
0,2715 |
| 0,0020 |
0,0287 |
0,0000 |
0,0405 |
0,2121 |
0,0000 |
0,1680 |
0,0000 |
0,2285 |
0,1682 |
0,1828 |
| 0,0030 |
0,0281 |
0,0000 |
0,1004 |
0,2627 |
0,0000 |
0,1658 |
0,0000 |
0,2188 |
0,1169 |
0,1355 |
| 0,0040 |
0,0297 |
0,0000 |
0,2041 |
0,3493 |
0,0000 |
0,1628 |
0,0000 |
0,2018 |
0,0288 |
0,0532 |
| 0,0050 |
0,0329 |
0,0387 |
0,2763 |
0,3917 |
0,0000 |
0,1263 |
0,0000 |
0,1671 |
0,0000 |
0,0000 |
| 0,0060 |
0,0378 |
0,0945 |
0,3707 |
0,4172 |
0,0000 |
0,0343 |
0,0000 |
0,0833 |
0,0000 |
0,0000 |
| 0,0070 |
0,0444 |
0,1599 |
0,4852 |
0,3548 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
| 0,0080 |
0,0544 |
0,2490 |
0,6419 |
0,1091 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
| 0,0085 |
0,0744 |
0,6889 |
0,3111 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
Źródło: obliczenia własne.
Na rysunku 2 zamieszczono graficzną prezentację otrzymanych portfeli wraz z portfelem fundamentalnym oznaczonym gwiazdką.
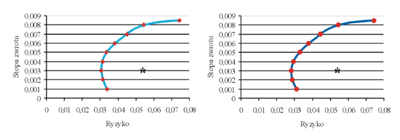
Rys. 2. Portfele zbudowane na podstawie modelu Markowitza (lewy) i na podstawie modelu Sharpe’a (prawy)
Źródło: opracowanie własne.
Jak widać z różnica między modelami Markowitza i Sharpe’a jest praktycznie niezauważalna. Wyraźnie natomiast odstaje od linii portfeli efektywnych (w sensie Markowitza) portfel fundamentalny, jednak jego prawdziwą efektywność należy ocenić na podstawie faktycznej stopy zwrotu, która powinna być pochodną „silnych fundamentów” spółek tworzących portfel w długim horyzoncie. Taką miarą jest właśnie Ep, wyznaczona na podstawie wzoru (10). Okazało się, że przy ryzyku jakie otrzymano dla fundamentalnego portfela 5,4% modele Markowitza i Sharpe’a dla ryzyka 5,4% wskazują na taki sam portfel, którego skład jest zamieszczony w tabeli 2. Z tego względu w dalszej części porównań dokonano dla modelu Markowitza. Zakupu akcji do budowy portfela klasycznego według modelu Markowitza i fundamentalnego dokonano w dniu 31 grudnia 2001 roku (na ten dzień przeprowadzono wcześniejszą analizę), a sprzedaży dokonano w dniu 3 kwietnia 2002 roku. Zakup został dokonany za kwotę 100 000 zł. W tabeli 3 podano oprócz udziałów akcji w portfelach również ceny zakupu i sprzedaży poszczególnych akcji, liczbę kupionych akcji w rozpatrywanych dwóch portfelach oraz zyski po sprzedaży obu portfeli. Obliczona została rzeczywista stopa zwrotu z przeprowadzonych transakcji (Ep) oraz stopa zwrotu z indeksu giełdowego WIG.
Tabela 3. Porównanie portfeli otrzymanych według metody Markowitza i Sharpe’a z portfelem fundamentalnym
| Wyszczególnienie |
COMPLAND |
PEKAO |
SWIECIE |
AGORA |
WIG |
|
Zakup [zł]
31.12.2001 |
105,0 |
79,9 |
28,8 |
51,4 |
13922,2 |
|
Sprzedaż [zł]
03.04.2002 |
117,5 |
103,0 |
28,5 |
61,6 |
14835,2 |
|
Model Markowitza
Sharpe’a (udziały) |
0,25 |
0,11 |
0,64 |
0 |
- |
|
Zakupiona liczba akcji |
238 |
138 |
2222 |
0 |
- |
|
Koszt zakupu [zł] |
25 000 |
11 000 |
64 000 |
0 |
100 000 |
|
Portfel fundamentalny
(udziały) |
0,08 |
0,49 |
0 |
0,43 |
- |
|
Zakupiona liczba akcji |
73 |
612 |
0 |
845 |
- |
|
Koszt zakupu [zł] |
7 710 |
48 870 |
0 |
43 420 |
100 000 |
|
Sprzedaż portfela
Markowitza/Sharpe’a |
27 976,19 |
14 180,23 |
63 333,33 |
0 |
105 489,7 |
|
Sprzedaż portfela
fundamentalnego |
8 627,857 |
62 998,87 |
0 |
52 036,42 |
123 663,2 |
| Stopa zwrotu: WIGu |
6,56% |
| portfela Markowitza |
5,49% |
portfela
fundamentalnego |
23,66% |
Źródło: obliczenia własne.
Z danych zamieszczonych w tabeli 3 wynika, że pomimo iż w świetle kryteriów Markowitza portfel fundamentalny nie należał do efektywnych, to pozwolił on na uzyskanie znacznie lepszego rezultatu. Portfel Markowitza był gorszy od indeksu giełdowego (7%) i dał po trzech miesiącach zaledwie 5% tygodniową stopę zwrotu, podczas gdy w tym samym czasie portfel fundamentalny pozwolił na uzyskanie 24% tygodniowej stopy zwrotu. Jest to prawie 5 razy więcej niż dla modelu Markowitza. Już ten prosty przykład pokazuje zasadność rozwijania badań nad fundamentalnym portfelem papierów wartościowych. Jeżeli za normę przyjmiemy stopę zwrotu dla indeksu giełdowego, lub średnie oprocentowanie depozytów tym okresie (od stycznia do marca 2002 roku) wówczas porównanie tych wielkości z Ep dla fundamentalnego portfela papierów wartościowych wskazuje, że jest to portfel efektywny. Oczywiście taki pomiar efektywności jest właściwy ze względu na porównania z klasycznym modelem Markowitza i jego pochodnymi. Właściwą efektywność fundamentalnego portfela powinno oceniać się dopiero po upływie co najmniej roku. Można wówczas z powodzeniem zastosować do takiego modelu układ danych miesięcznych dla wyznaczania stopy zwrotu i ryzyka dla poszczególnych akcji.
Literatura
Tarczyński W.: Taksonomiczna miara atrakcyjności inwestycji w papiery wartościowe. „Przegląd Statystyczny” 1994, nr 3.
Tarczyński W., Hozer J., Gazińska M., Wawrzyniak K.: Analiza fundamentalna na giełdzie papierów wartościowych. PTE, Szczecin 1995a.
Tarczyński W.: O pewnym sposobie wyznaczania składu portfela papierów wartościowych. „Przegląd Statystyczny” 1995b, nr 1.
Tarczyński W.: Analiza portfelowa na giełdzie papierów wartościowych. PTE, Szczecin 1996.
Tarczyński W.: Rynki kapitałowe, metody ilościowe. Vol. 2, Placet, Warszawa 1997.
Tarczyński W.: Rynki kapitałowe, metody ilościowe. Vol. 1, Placet, wyd.2, Warszawa 2001.
Tarczyński W.: Fundamentalny portfel papierów wartościowych, PWE, Warszawa 2002.
|